Definición
La sucesión de números complejos {zn}∞
n=0 tiene un límite o converge a un
número complejo z, si para todo ε > 0 existe un número entero positivo N tal que
|zn − z| < ε siempre que n > N.
Cuando el límite de la sucesión {zn}∞ n=0 existe, es decir, que {zn}∞ n=0 converge a z, se escribe
lim n→∞ zn = z.
Si la sucesión no tiene límite diverge.
Teorema
Sean zn = xn + iyn (n = 0, 1, 2, . . . ), para xn y yn numer ´ os reales, y z = x + iy
para x y y numer ´ os reales. Entonces, limn→∞ zn = z si, y s´olo si limn→∞ xn = x y limn→∞ yn = y.
Ejemplo Determinar si la sucesión
zn = 1/n
+ i(1 + (−1)n/ n) (n = 1, 2, 3, . . . )
converge y halle el líımite si es el caso.
Solución. Se tiene que
zn = xn + iyn, donde
xn = 1/n, yn = 1 +( (−1)n/ n) .
Ahora,
limn→∞ xn = 0 y limn→∞ yn = 1.
Por el Teorema la sucesión zn = 1/n + i(1 + ((−1)n/ n)
converge y, además,
lim n→∞ zn = i.
Integrales de funciones de variable compleja
Si Ω es un dominio en el plano complejo y f : Ω → C es una función de variable compleja, ¿cómo
podríamos definir la integral de f entre dos puntos z1 y z2 de Ω, digamos R z2
z1 f(z) dz?
Cuando se define la integral R x2
x1 f(x) dx de una función de variable real, nos valemos de la
noción intuitiva de área construyendo aproximaciones cada vez mejores del área de la región
comprendida entre la curva de ecuación y = f(x) y el intervalo [x1, x2] del eje OX mediante
sumas finitas de la forma Pn f(xn)∆xn cada una de las cuales corresponde a una partición del
intervalo [x1, x2]. Para extender este proceso a integrales de funciones complejas nos encontramos
con dos dificultades. La primera es que ahora no tenemos la noción intuitiva de integral como
área y la segunda es que para ir de z1 a z2 podemos seguir muchas curvas (sin salirnos del dominio
Ω) y cada curva podría proporcionar (tras el proceso de hacer particiones, construir las sumas y
tomar límites) un valor diferente de la integral.
Sabemos que la integral de línea de un campo vectorial real plano F (x, y) entre dos puntos
(x1, y1) y (x2, y2) no depende del camino utilizado para ir desde el primer punto hasta el segundo
cuando el campo es conservativo. En consecuencia, podremos definir integrales de funciones de
variable compleja que sólo dependan de los puntos entre los que integremos, y no del camino
usado para ir de uno a otro, cuando, al realizar la identificación de una función de variable
compleja con un par de funciones reales de dos variables, el campo vectorial que aparezca en la
integral de línea sea conservativo. Fueron C. F. Gauss y A. L. Cauchy quienes descubrieron que
las funciones de variable compleja que cumplen esta condición son, precisamente, las funciones
analíticas.
Curvas en el plano complejo. Una curva parametrizada en el plano complejo C es la imagen
de una función continua con valores complejos z(t) = x(t) + jy(t) definida para los puntos t de
un intervalo [t1, t2] ⊂ R. La variable independiente t de la función z(t) se llama parámetro de
la curva y la propia función z(t) recibe el nombre de parametrización de la curva. Los puntos
z1 = z(t1) y z2 = z(t2) se llaman extremos de la curva; z1 es el extremo de partida y z2 es el
extremo de llegada (por eso en algunos textos no se habla de curvas en el plano complejo, sino
de caminos). Naturalmente, una curva z(t) en el plano complejo C se identifica con la curva
(x(t), y(t)) en el plano real, lo que nos permite trasladar de manera obvia a curvas complejas
algunos conceptos dados para curvas planas como los de curva simple (la que no se cruza consigo
misma salvo, quizás, en los extremos), curva cerrada (cuando sus extremos coinciden), curva
regular o suave (cuando las funciones x(t) e y(t) son derivables con derivada continua en [t1, t2],
en cuyo caso se define z0
(t) = x0
(t) +jy0
(t)), curva regular o suave a trozos (cuando las funciones
x(t) e y(t) son derivables con derivada continua en [t1, t2] salvo en un número finito de valores
del parámetro que corresponden a esquinas de la curva) o curva de Jordan (una curva regular a
trozos, cerrada y simple).
Derivación Compleja
Sea f una función cuyo dominio contiene un entorno
del punto z0. La derivada de f en z0 se define como:
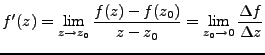
Siempre que este límite exista. Cuando existe la
derivada de f en z0 se dice que f es derivable en z0.
La derivada, com en el caso real, es el límite de un cociente incremental. Que la funciónf(z) sea derivable en
zo significa que para cualquier trayectoria de aproximación a zo el límite del cociente incremental es siempre un mismo número complejo.
Ejemplo
La función f(z) = 2z + 3i es derivable en todo z ∈ℂ.
Si z = x + yi, z0 = x0 + y0i, el cociente incremental es f(z) -f(z0) z -z0 = 2x + (2y + 3)i -2x0 -(2y0 + 3)i x + yi -(x0 + y0i) = 2[(x -x0) + (y -y0)i] (x -x0) + (y -y0)i = 2
Por tanto,
limz→z0 f(z) -f(z0) z -z0 = 2 para cualquier trayectoria.
La función z no es derivable en ningún punto.
Por tanto,
limz→z0 f(z) -f(z0) z -z0 = 2 para cualquier trayectoria.
La función z no es derivable en ningún punto.
Si escribimos en forma binaria z = x + yi, f(x + yi) = x -yi y z0 = x0 + y0i, el cociente incremental es: f(z) -f(z0) z -z0 = x -yi -(x0 -y0i) x + yi -(x0 + y0i) = (x -x0) -(y -y0)i (x -x0) + (y -y0)i
En este caso el límite limz→z0 f(z) -f(z0) z -z0 no existe globalmente, ya que las diferentes trayectorias rectilíneas por las cuales nos podemos acercar a z0 dan valores diferentes para el límite
En este caso el límite limz→z0 f(z) -f(z0) z -z0 no existe globalmente, ya que las diferentes trayectorias rectilíneas por las cuales nos podemos acercar a z0 dan valores diferentes para el límite
Funciones analíticas
Una función f(z) es analítica en un
punto z0 si existe una vencidad |z−z0|<δ
tal que en cada punto de la vecindad
exista f′(z)
Una función analítica es aquella que puede expresarse como una serie de potencias convergente. Una función analítica es suave si tiene infinitas derivadas. La noción de función analítica puede definirse para funciones reales o complejas, aunque ambos conjuntos tienen propiedades distintas. Las funciones complejas derivables en un abierto siempre son analíticas, y se denominan funciones holomorfas. Sin embargo, una función real infinitamente derivable no es necesariamente analítica.
Una función real (compleja) f es analítica en un punto x0 de su dominio si existe una serie de potencias centrada en x0:
que converge en un entorno U ⊆ R (U ⊆ C) de x0 y que coincide con la función en dicho entorno:
Una función analítica en x0 es infinitamente derivable en un cierto entorno U de dicho punto, en el que además su serie de Taylor:
converge (y coincide con f).





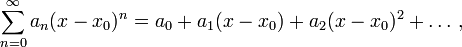
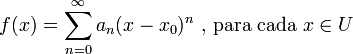




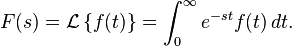

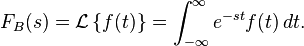
 es llamado el operador de la transformada de Laplace.
es llamado el operador de la transformada de Laplace.




