Transformadas de Laplace

 Transformada de Laplace

La transformada de Laplace es un tipo de transformada integral frecuentemente usada para la resolución de ecuaciones diferenciales ordinarias. La transformada de Laplace de una función f(t) definida (en ecuaciones diferenciales, en análisis matemático o en análisis funcional) para todos los números positivos t ≥ 0, es la función F(s), definida por:






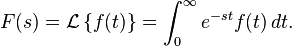
siempre y cuando la integral esté definida. Cuando f(t) no es una función, sino una distribución con una singularidad en 0, la definición es






Cuando se habla de la transformada de Laplace, generalmente se refiere a la versión unilateral. También existe la transformada de Laplace bilateral, que se define como sigue:






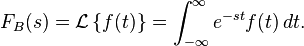
La transformada de Laplace F(s) típicamente existe para todos los números reales s > a, donde a es una constante que depende del comportamiento de crecimiento de f(t).

es llamado el operador de la transformada de Laplace.

 

Definición de la Transformada Inversa 

 La Transformada inversa de una función en s, digamos F(s) es una función de t cuya transformada es precisamente F(s), es decir

si es que acaso

Esta definición obliga a que se cumpla:

y

Cómo Resolver Transformadas